Equations Describing Normal Attack by Kinetic Energy Projectiles

he processes involved in penetration of armour are complex and analysis of them in detail leads to elaborate mathematical models which are only amenable to numerical solutions involving computer programmes. Simple analytical models provide little insight into the process of penetration and their validity is restricted but within their range they can predict penetration with considerable accuracy.³

The most common example of such a model is the following relationship between the mass, diameter and velocity of a particular type of projectile and the corresponding thickness of a given kind of armour which the projectile perforates at normal impact:³

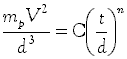. . . . . . (1)

where m_p = mass of projectile (kg);
           V = velocity of the projectile at impact (m/s);
            t = thickness of armour perforated (mm);
            d = diameter of projectile (mm); and
        C, n = constants.

A similar equation with n = 1 is obtained if the assumption is made that the kinetic energy of a projectile is absorbed in creating a hole in the armour by moving the material sideways. Another equation of the same kind but with n = 2 is obtained by assuming that the kinetic energy of a projectile is absorbed in pushing out of the armour a cylindrical plug of the same diameter as the projectile.³

Neither of the above hypotheses corresponds exactly to what happens but when equation (1) is fitted to the observed results the values of the index n generally fall between 1 and 2.³ A modified version of this formula using n = 1.43 was widely used in Britain in World War II.¹ Formulæ of this form are commonly referred to as de Marre formulæ, after J. de Marre who first devised a similar formula around 1886.

There are many different forms of equation (1) because the parameters C and n which appear in it vary with the geometry and the material of the projectile and with the armour of the target. They can only be considered as constants, therefore, when particular projectile and armour combinations are involved. Thus, when the results of firing APCBC projectiles from a gun such as the 83.8mm 20-pounder at RHA are correlated equation (1) becomes:³

However, when the projectile is APDS, such as that fired from the 105mm L7, or M68, gun and again at RHA equation (1) becomes:³

In equation (3) the mass and diameter are not those of the projectile as fired from the gun, or even of it in flight, but the considerably smaller mass and diameter of the high density tungsten penetrator which perforates the armour. Of the mass of the projectile at the instant of firing, its launch or internal ballistics mass, 21% to 31% is accounted for by the sabot. Of the remaining in-flight, or external ballistics, mass 20% to 30% consists of the mass of the penetrator sheath. Consequently, the mass of a typical APDS penetrator amounts to only 54% of the launch mass. Likewise, the in-flight diameter of a typical 105mm APFSDS projectile is only 60mm and the diameter of its penetrator is 44mm.³

Similar comments apply to APFSDS projectiles but their sabots account for an even greater percentage of the launch mass than the pot type sabots of APDS projectiles. The usual APFSDS sabots are of the so-called saddle, or, more accurately, spool type and they account for 30% to 40%, or even 50% of the launch mass. The relative mass of the sabots tends to increase with the muzzle velocity of the projectiles, because of the need to make them stronger to withstand the correspondingly higher pressures and maximum accelerations. On the other hand, the mass of the APFSDS penetrators is not much less than the in-flight mass of the projectile, the relatively small difference between the two being due to the nose shield and the fins.³

Correlation of the results obtained with APFSDS projectiles in terms of equation (1) produces widely differing values of the parameters C and n, even when the penetrator and target materials are the same, because of the wide variation in geometry of their penetrators. Attempts have been made to generalise equation (1) by rewriting it to include explicitly the ratio of the penetrator length to its diameter but no generally accepted expression has been devised for the dependence of C and n on this ratio. Almost all that can be said is that n tends to decrease and C to increase with the length to diameter ratio. This is consistent with the fact that the depth of penetration increases with the length to diameter ratio, which might be expected intuitively because kinetic energy per unit area of the target increases with it.³

Do you like this web site? Please rate it between one and ten, with ten being the best:

The Mechanism of Plate Penetration and Failure

Equations Describing Normal Attack by Kinetic Energy Projectiles