Logo from Scott Cunningham.
Logo from Scott Cunningham.
arlier in this article a model of the relationship between the mass, diameter and velocity of a particular type of projectile and the corresponding thickness of a given kind of armour which the projectile perforates at normal impact was given as equation (1). The effect of oblique angles of attack on conventional steel projectiles was given by equation (4) and gives the best agreement for angles from 0° to 30°:1
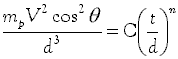. . . . . . (4)
where mp = mass of projectile (kg);
V = velocity of the projectile at impact (m/s);
= angle of attack;
t = thickness of armour perforated (mm);
d = diameter of projectile (mm); and
C, n = constants.
For angles greater than 30° penetration becomes less than that given by equation (4). Rearranging equation (4) the thickness penetrated by a given conventional steel projectile at a given impact velocity is proportional to:
. . . . . . (5)
Britain in World War II used n = 1.43 [1], so using this as an average for a given conventional steel projectile we find that:
. . . . . . (6)
It is important to remember that the thickness t is measured perpendicular to the armour plate, i.e., it is not the line of sight thickness. At higher angles than 30° the power of the cosine will increase, leading to a further decrease in penetration. Also the relationship described by equation (6) relies on using n = 1.43, and that is simply not true for all projectiles at all values of T/D ratio. Equation (6) is only a rough approximation.
World War II sub-calibre projectiles suffered more from obliquity than conventional steel projectiles. British World War II sub-calibre projectiles sheathed the brittle core with steel reducing but not eliminating this effect; they were still worse affected by oblique attacks than conventional steel projectiles. Equation (4) provided a good fit to observed results for British projectiles, for angles from 0° to 30°, with the constant n reduced from 1.43 to more nearly unity.1 This is also true for post World War II APDS up to and including the 105mm L22 projectile.3 Substituting n = 1 into equation (5) we get for early British sub-calibre projectiles:
. . . . . . (7)
The same caution described above for equation (6) also applies to equation (7). Equation (7) is only a rough approximation.
Post World War II APDS projectiles, from the 105mm L28 projectile (and its USA counterpart the M392) onwards, sufferred to a much lesser extent from obliquity, close to but not quite as good as other kinetic energy projectiles, due to better design. The thickness of armour penetrated is proportional to:3
. . . . . . (8)
For APFSDS projectiles, there is no effect to their line of sight penetration due to obliquity up to about 70°; for HEAT projectiles there is no effect to their line of sight penetration due to obliquity at any angles.3 So the thickness of armour penetrated is proportional to:
. . . . . . (9)
Do you like this web site? Please rate it between one and ten, with ten being the best:
Ratings are submitted to: The Wargames and Military History Search Engine.
